Suite au lancement de la fabrication du vélo-rail, nous avons étudié la transmission de celui-ci. Cela nous a permis d'utiliser quelques notions mathématiques comme les grandeurs proportionnelles et les grandeurs inversement proportionnelles ainsi que des calculs de vitesse.

Rappel des différentes grandeurs :

	Définition		Propriété	Graphique
Grandeurs Proportionnelles		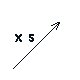	Rapport constant	Droite passant par l'origine du repère
Grandeurs Inversement Proportionnelles		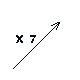	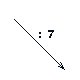Produit constant	Hyperbole

1. Schéma du "Vélo-rail"

2. Développement du "Vélo-rail"

Le développement du vélo-rail correspond à la distance parcourue quand le pédalier fait un tour.

       a) nombre de tours du pignon (de la roue) pour un tour de pédalier.

Tableau :

grandeurs inversement proportionnelles

49 x 1 = 18 x X

X = 49/18

X = 2,72 tours

Donc quand le pédalier fait un tour, le pignon lui a fait 2,72 tours.

(et la roue également !!!).

        b) Calcul du développement :

P = p x 0,2 m P = 0.628 m

Le perimètre de la roue est de 0.628 mètre.

D = P x 2,72 (périmètre de la roue)

D = 1,70816 m

Le développement est alors de 1,71 m .

3. Calcul de la vitesse de déplacement : pour 1.5tr/s du pédalier

formule de base V = d / t

V : Vitesse en km/h

d : Distance en mètre

t : Temps en heure

Calcul de D ?

D = 1,5 x 1,71

D = 2,565 m

En une seconde, la distance parcourue est de 2,565 mètres.

V = 2.565m/s

V = 0.002565km x 3600

V = 9,234 km/h

Calcul de V ?

V = 0.002565km / 3600s

V = (0.002565 x 3600) / 1 V = 9,234 km/h

En conclusion, la vitesse du vélo-rail serait de 9,234 km/h pour 1,5 tr/s du pédalier.